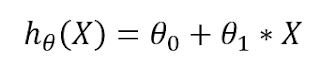Hi Friends,
Welcome again,
Today We are going to learn about Regression. We have already learn a brief about regression. But now, we take deep dive into the regression. It is a very broad thing in ML.
So, let's start with regression.
Regression is a type of supervised learning, so it has input variable as well as output variable like classification, but regression works for statistical analysis on data. or we can say it is a statistical process to estimate real values, such as, prices of different cars.
Lets take an example of regression:
Welcome again,
Today We are going to learn about Regression. We have already learn a brief about regression. But now, we take deep dive into the regression. It is a very broad thing in ML.
So, let's start with regression.
Regression is a type of supervised learning, so it has input variable as well as output variable like classification, but regression works for statistical analysis on data. or we can say it is a statistical process to estimate real values, such as, prices of different cars.
Lets take an example of regression:
import csv
import numpy
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn import svm
import numpy
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn import svm
file_name="regression_ex.csv"
raw_data=open(file_name,"rt")
reader=csv.reader(raw_data,delimiter=',',quoting=csv.QUOTE_NONE)
x=list(reader)
data=numpy.array(x)
reader=csv.reader(raw_data,delimiter=',',quoting=csv.QUOTE_NONE)
x=list(reader)
data=numpy.array(x)
plt.scatter(data[1:,0],data[1:,1])
Output:
| Figure: Regression of Month wise Heatwave |
So, This is a simple example of regression. in next article, we will learn different types of regression.