Hello Friends!!!
Today in this article, we are going to learn about Naive Bayes Classifier, One more algorithm for classification. It is based on Bayes' theorem.
So, first of all, let's take a look at Bayes' theorem, this theorem is based on conditional probability.
What is Conditional Probability?
The probability which is assigned to an event A when it is known that another event B has occurred, or which would be assigned to A if it was known that B had occurred, which is known as "Conditional Probability" of A given to B. For example, the probability of getting raincoat in the market is connected with season.
P(A|B) - represents the conditional probability of the event A given the event B; the probability assigned to A when it is known that the event B has occurred;
P(A,B) - represents the joint probability of event A and event B; i.e. the probability that both events A and B will occur.
(Resource: Probability and Statistics
for Business Decisions By Robert Schlaifer Professor of business administration Harvard University)
Now, we move to Bayes' theorem:
Bayes' theorem is used to describe the probability of an event based on some condition that may be related to an event.
When we apply Bayes' theorem, it checks how the degree of beliefs, expressed as a probability. It also accounting evidence.
Let's understand the equation,
Here, P(A|B) represents a conditional probability, shows when the probability of an event A occurring given that event B is true.
same as with P(B|A) also a conditional probability, shows when the probability of an event B occurring given that event A is true.
P(A) and P(B) both are the probabilities of observing A and B independently and there is no relation with each other.
One more thing with this formula is: P(B) should not be 0.
For example,
In any medical test, such as Diabetes, the test is positive or negative. if the test is positive, detects diabetes otherwise not. we put this situation in the above equation.
P(A)=Diabetes detected
P(B)=Test is positive
P(B|A)=(Test = Positive | Diabetes = True)
P(A|B)=P(B|A)*P(A)/P(B)
P(Diabetes = True | Test = Positive)= P(Test = Positive | Diabetes = True)*P(Diabetes = True) / P(Test = Positive)
That's it for this article in the next article we will learn Naive Bayes' theorem. I hope, you learn new things from this article...
Happy Learning....☺😊
Today in this article, we are going to learn about Naive Bayes Classifier, One more algorithm for classification. It is based on Bayes' theorem.
So, first of all, let's take a look at Bayes' theorem, this theorem is based on conditional probability.
What is Conditional Probability?
The probability which is assigned to an event A when it is known that another event B has occurred, or which would be assigned to A if it was known that B had occurred, which is known as "Conditional Probability" of A given to B. For example, the probability of getting raincoat in the market is connected with season.
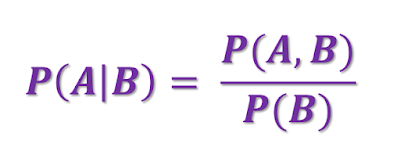 |
| Mathematical Definition of Conditional Probability |
P(A,B) - represents the joint probability of event A and event B; i.e. the probability that both events A and B will occur.
(Resource: Probability and Statistics
for Business Decisions By Robert Schlaifer Professor of business administration Harvard University)
Now, we move to Bayes' theorem:
Bayes' theorem is used to describe the probability of an event based on some condition that may be related to an event.
 | ||
| Fig. 2 Bayes' theorem equation |
Let's understand the equation,
Here, P(A|B) represents a conditional probability, shows when the probability of an event A occurring given that event B is true.
same as with P(B|A) also a conditional probability, shows when the probability of an event B occurring given that event A is true.
P(A) and P(B) both are the probabilities of observing A and B independently and there is no relation with each other.
One more thing with this formula is: P(B) should not be 0.
For example,
In any medical test, such as Diabetes, the test is positive or negative. if the test is positive, detects diabetes otherwise not. we put this situation in the above equation.
P(A)=Diabetes detected
P(B)=Test is positive
P(B|A)=(Test = Positive | Diabetes = True)
P(A|B)=P(B|A)*P(A)/P(B)
P(Diabetes = True | Test = Positive)= P(Test = Positive | Diabetes = True)*P(Diabetes = True) / P(Test = Positive)
That's it for this article in the next article we will learn Naive Bayes' theorem. I hope, you learn new things from this article...
Happy Learning....☺😊
.png)



No comments:
Post a Comment